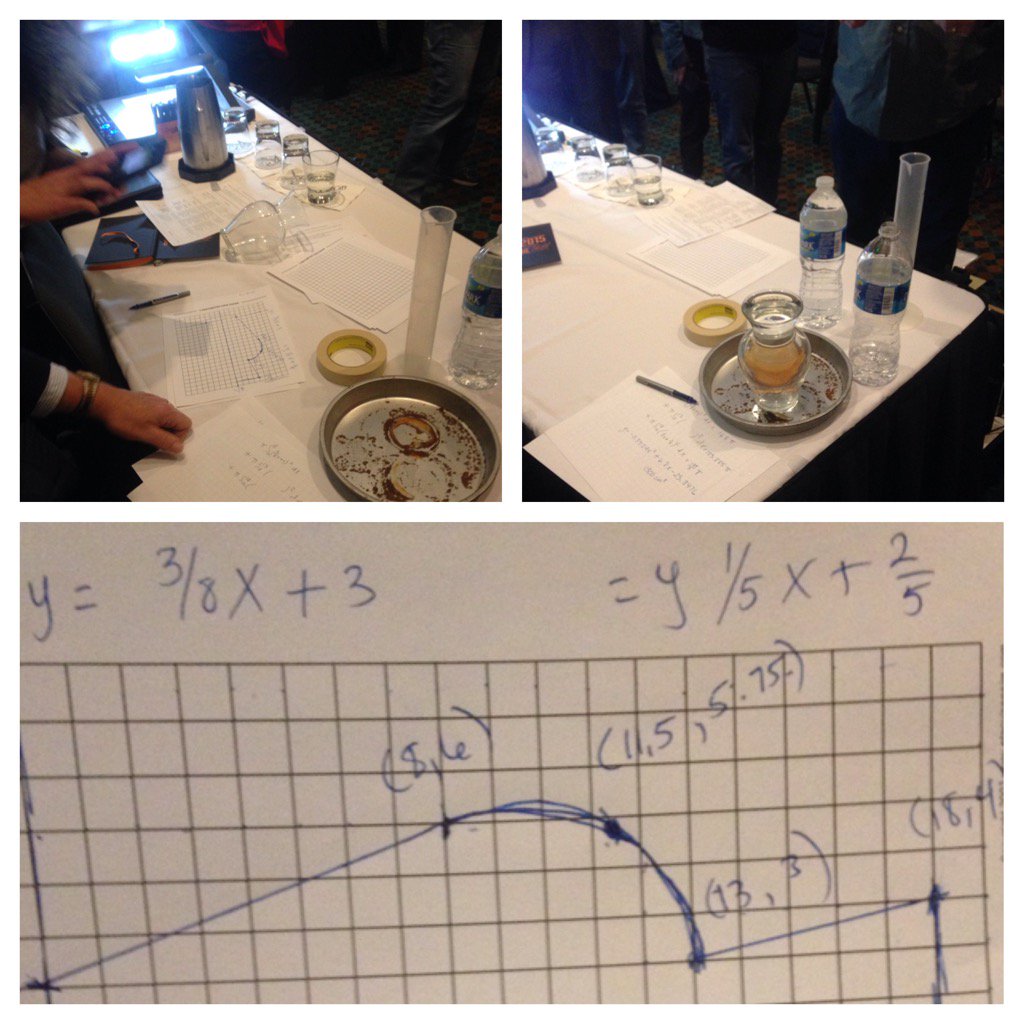
Here is an activity that I created for our class review today so I could pull together some small groups. I printed them front to back (they line up when printed), then cut a set for each small group:
The rules are this:
- Students play in 2 vs. 2 games (so 4 students per group)
- Students look at the 1st card and work with their partner to solve the problem completely on their whiteboard or in their notes
- First group to have a complete solution written can "slap" the deck to indicate they're done. They then have to defend their answer. If they're right, they get to keep the card. If not, the other group gets a chance to "steal" by getting the question right.
- If no one gets it right, the whole group has to work to figure the problem out. No one gets the card, but they're still responsible for the topic.
- Group with the most cards at the end wins!
I also gave each group a stack of red, yellow, and green cups to indicate if they needed help or not. Thank you, Math=Love for this great idea!
What worked?
- It's easy to differentiate by removing certain questions from the deck for some groups or by adding in enrichment cards (which I need to get around to making) for the stronger groups
- I can move around the room or pull small groups aside and the activity flows pretty smoothly
- Some groups chose to not actually play the game. Instead, they decided to sort them by what was easy and what was hard and go through the harder ones.
- The cups!! The cups!! Seriously, if you don't already do this, start. It will stop you from hearing your name frantically 47,214 times in the same period.
What needs improvement?
- I will definitely group more strategically next time. I had 1 or 2 kids who were fish out of water with their group and were scared to use the cup to indicate they were confused if no one else was.
- I honestly needed a prize to rush them a little bit more to "play"- some kids take it so seriously, they can't have fun with it
Overall, another awesome day with my kiddos!