Disclaimer: This is a brainstorm....brain dump....random collection of ideas that I hope other amazing AP Calc teachers might be able to expand upon? I offer no solutions in this post...just questions.
We are getting 2 new 3D printers next week and have a training on using them (YES!) and there is obviously a direct relationship to all the applications of volume we discuss in AP Calc. I've done some searching....which always just leads to more questions and ideas. I started from watching these 2 videos:
Solids of Revolution
 |
| NCTM Performance Task |
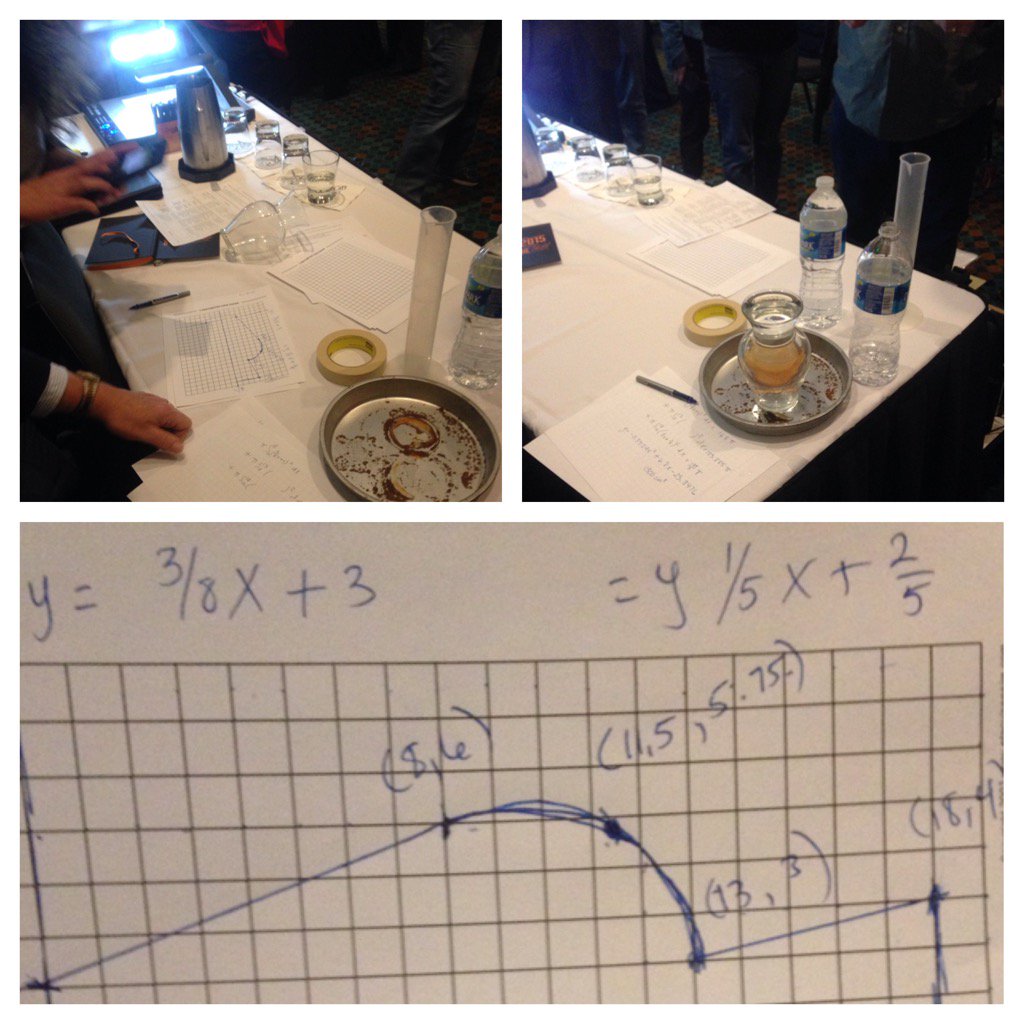
Cross Sectional Volumes
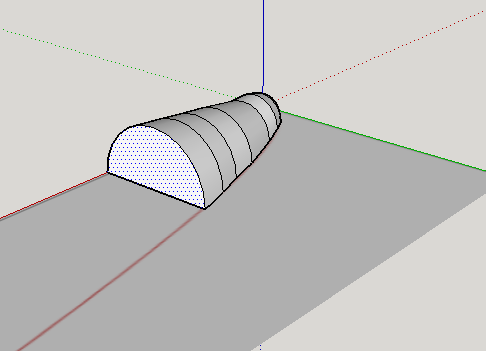
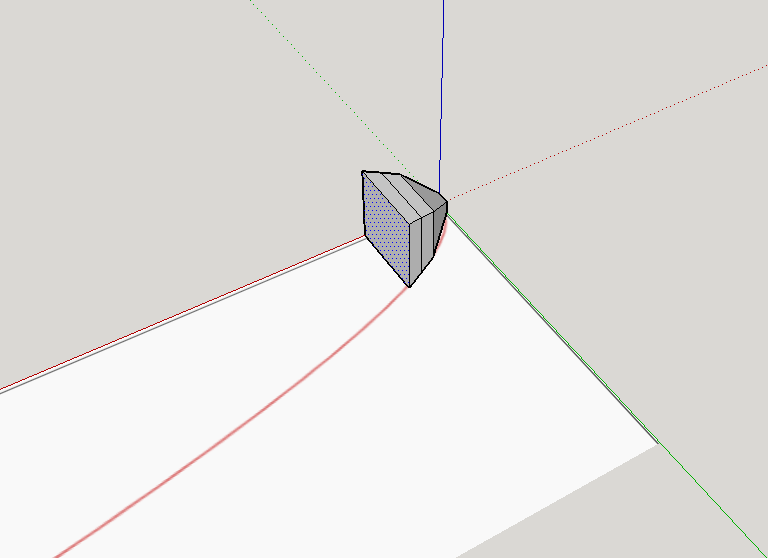 Logistically, I actually think this is easier. In about 15 minutes of playing around I was able to create 2 designs that would model different cross sections. My kids have experience with 3D printing...this wouldn't be mind blowing for them. My struggle is having them print 3D models seems like the thing I hate most....a project for the sake of doing a project. Might it be a fun way to spend some time after the AP exam? Sure. But if I want to invest any time in this, I want it to be something that's worthwhile mathematically as well. I want something that can be low-floor, high-ceiling since our school ranges in ability level from Honors Calculus to BC Calculus (to a kid who is taking an MIT Quantum Physics MOOC for fun....seriously). Can you tell that I have lofty goals here?
Logistically, I actually think this is easier. In about 15 minutes of playing around I was able to create 2 designs that would model different cross sections. My kids have experience with 3D printing...this wouldn't be mind blowing for them. My struggle is having them print 3D models seems like the thing I hate most....a project for the sake of doing a project. Might it be a fun way to spend some time after the AP exam? Sure. But if I want to invest any time in this, I want it to be something that's worthwhile mathematically as well. I want something that can be low-floor, high-ceiling since our school ranges in ability level from Honors Calculus to BC Calculus (to a kid who is taking an MIT Quantum Physics MOOC for fun....seriously). Can you tell that I have lofty goals here?
So here's where I need my MTBoS friends...
What sort of tasks and applications do you associate with this topic?
I want to do more than just create a model, so how can I challenge my kids with creating a model within given constraints and do it meaningfully? My coworker and I have been trying to think of how to get kids to apply this concept in the real world and really use the model to serve a purpose.
Please feel free to share, comment, and question!! We promise to tell you where this road leads us and share any resources along the way!
No comments:
Post a Comment